Prim算法实现最小生成树(C语言)
Prim算法是一种用于寻找无向图最小生成树的贪心算法,下面我将提供一个完整的C语言实现。
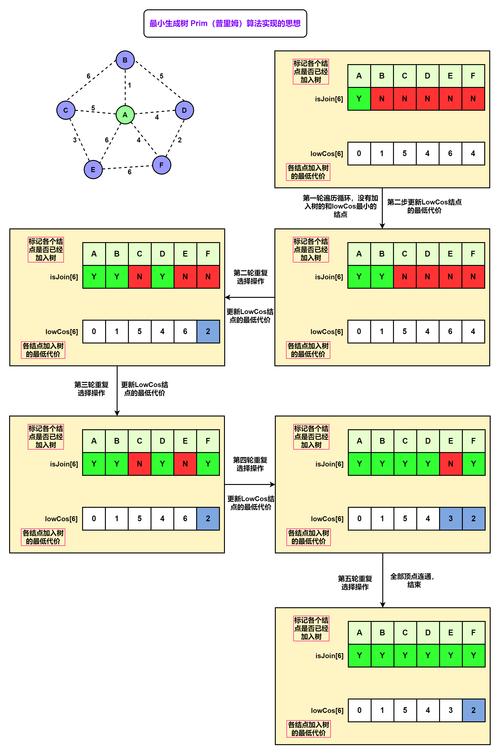
(图片来源网络,侵删)
算法思路
- 从任意一个顶点开始,将其加入生成树集合
- 重复以下步骤直到所有顶点都加入生成树:
- 在生成树集合外的顶点中,找到与生成树集合连接的最小权边
- 将该边及其顶点加入生成树集合
- 更新其他顶点到生成树的最小距离
C语言实现
#include <stdio.h>
#include <limits.h>
#include <stdbool.h>
#define V 5 // 顶点数量
// 找到未包含在MST中的顶点中key值最小的顶点
int minKey(int key[], bool mstSet[]) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// 打印构建的MST
void printMST(int parent[], int graph[V][V]) {
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++) {
printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]);
}
}
// 使用Prim算法构建MST
void primMST(int graph[V][V]) {
int parent[V]; // 存储构建的MST
int key[V]; // 存储到MST的最小权重
bool mstSet[V]; // 顶点是否包含在MST中
// 初始化所有key值为无穷大,mstSet[]为false
for (int i = 0; i < V; i++) {
key[i] = INT_MAX;
mstSet[i] = false;
}
// 第一个顶点总是MST的根
key[0] = 0;
parent[0] = -1; // 第一个节点没有父节点
// 构建MST,V-1条边
for (int count = 0; count < V - 1; count++) {
// 找到未包含在MST中的顶点中key值最小的顶点
int u = minKey(key, mstSet);
// 将选定的顶点加入MST集合
mstSet[u] = true;
// 更新与u相邻的顶点的key值和parent值
for (int v = 0; v < V; v++) {
// graph[u][v]非零,v不在MST中,且graph[u][v]小于key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
// 打印构建的MST
printMST(parent, graph);
}
int main() {
/* 示例图 */
int graph[V][V] = {
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}
};
primMST(graph);
return 0;
}
代码说明
-
数据结构:
graph[V][V]: 邻接矩阵表示的图key[]: 存储每个顶点到MST的最小权重mstSet[]: 标记顶点是否已包含在MST中parent[]: 存储MST的结构
-
主要函数:
minKey(): 找到未包含在MST中的顶点中key值最小的顶点primMST(): Prim算法主函数printMST(): 打印生成的MST
-
时间复杂度:
- 使用邻接矩阵: O(V²)
- 使用邻接表和优先队列: O(E + V log V)
示例输出
对于给定的示例图,程序输出将是:
(图片来源网络,侵删)
Edge Weight
1 - 0 2
2 - 1 3
3 - 0 6
4 - 1 5 这表示最小生成树由以下边组成:
- 顶点1-顶点0,权重2
- 顶点2-顶点1,权重3
- 顶点3-顶点0,权重6
- 顶点4-顶点1,权重5
优化版本(使用优先队列)
对于稀疏图,可以使用优先队列来优化时间复杂度:
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define V 5
typedef struct MinHeapNode {
int v;
int key;
} MinHeapNode;
typedef struct MinHeap {
int size;
int capacity;
int *pos;
MinHeapNode **array;
} MinHeap;
MinHeapNode* newMinHeapNode(int v, int key) {
MinHeapNode* node = (MinHeapNode*)malloc(sizeof(MinHeapNode));
node->v = v;
node->key = key;
return node;
}
MinHeap* createMinHeap(int capacity) {
MinHeap* heap = (MinHeap*)malloc(sizeof(MinHeap));
heap->pos = (int*)malloc(capacity * sizeof(int));
heap->size = 0;
heap->capacity = capacity;
heap->array = (MinHeapNode**)malloc(capacity * sizeof(MinHeapNode*));
return heap;
}
void swapMinHeapNode(MinHeapNode** a, MinHeapNode** b) {
MinHeapNode* t = *a;
*a = *b;
*b = t;
}
void minHeapify(MinHeap* heap, int idx) {
int smallest, left, right;
smallest = idx;
left = 2 * idx + 1;
right = 2 * idx + 2;
if (left < heap->size && heap->array[left]->key < heap->array[smallest]->key)
smallest = left;
if (right < heap->size && heap->array[right]->key < heap->array[smallest]->key)
smallest = right;
if (smallest != idx) {
MinHeapNode *smallestNode = heap->array[smallest];
MinHeapNode *idxNode = heap->array[idx];
heap->pos[smallestNode->v] = idx;
heap->pos[idxNode->v] = smallest;
swapMinHeapNode(&heap->array[smallest], &heap->array[idx]);
minHeapify(heap, smallest);
}
}
int isEmpty(MinHeap* heap) {
return heap->size == 0;
}
MinHeapNode* extractMin(MinHeap* heap) {
if (isEmpty(heap))
return NULL;
MinHeapNode* root = heap->array[0];
MinHeapNode* lastNode = heap->array[heap->size - 1];
heap->array[0] = lastNode;
heap->pos[root->v] = heap->size - 1;
heap->pos[lastNode->v] = 0;
--heap->size;
minHeapify(heap, 0);
return root;
}
void decreaseKey(MinHeap* heap, int v, int key) {
int i = heap->pos[v];
heap->array[i]->key = key;
while (i && heap->array[i]->key < heap->array[(i - 1) / 2]->key) {
heap->pos[heap->array[i]->v] = (i - 1) / 2;
heap->pos[heap->array[(i - 1) / 2]->v] = i;
swapMinHeapNode(&heap->array[i], &heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
bool isInMinHeap(MinHeap *heap, int v) {
if (heap->pos[v] < heap->size)
return true;
return false;
}
void printMST(int parent[], int graph[V][V]) {
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]);
}
void primMST(int graph[V][V]) {
int parent[V];
int key[V];
MinHeap* heap = createMinHeap(V);
for (int v = 1; v < V; v++) {
parent[v] = -1;
key[v] = INT_MAX;
heap->array[v] = newMinHeapNode(v, key[v]);
heap->pos[v] = v;
}
heap->array[0] = newMinHeapNode(0, key[0]);
heap->pos[0] = 0;
key[0] = 0;
heap->size = V;
while (!isEmpty(heap)) {
MinHeapNode* minHeapNode = extractMin(heap);
int u = minHeapNode->v;
for (int v = 0; v < V; v++) {
if (graph[u][v] && isInMinHeap(heap, v) && graph[u][v] < key[v]) {
key[v] = graph[u][v];
parent[v] = u;
decreaseKey(heap, v, key[v]);
}
}
}
printMST(parent, graph);
}
int main() {
int graph[V][V] = {
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}
};
primMST(graph);
return 0;
}
这个优化版本使用最小堆来提高效率,特别适合处理稀疏图。
(图片来源网络,侵删)




